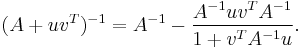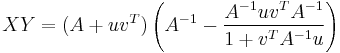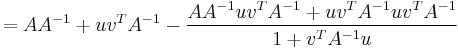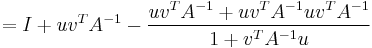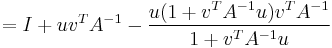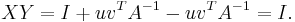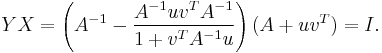Sherman–Morrison formula
In mathematics, in particular linear algebra, the Sherman–Morrison formula,[1][2][3] named after Jack Sherman and Winifred J. Morrison, computes the inverse of the sum of an invertible matrix  and the dyadic product,
and the dyadic product, 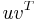 , of a column vector
, of a column vector  and a row vector
and a row vector 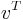 . The Sherman–Morrison formula is a special case of the Woodbury formula. Though named after Sherman and Morrison, it appeared already in earlier publications [4]
. The Sherman–Morrison formula is a special case of the Woodbury formula. Though named after Sherman and Morrison, it appeared already in earlier publications [4]
Contents |
Statement
Suppose  is an invertible square matrix and
is an invertible square matrix and  ,
,  are vectors. Suppose furthermore that
are vectors. Suppose furthermore that 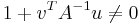 . Then the Sherman–Morrison formula states that
. Then the Sherman–Morrison formula states that
Here, 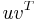 is the dyadic product of two vectors
is the dyadic product of two vectors  and
and  . The general form shown here is the one published by Bartlett.[5]
. The general form shown here is the one published by Bartlett.[5]
Application
If the inverse of  is already known, the formula provides a numerically cheap way to compute the inverse of
is already known, the formula provides a numerically cheap way to compute the inverse of  corrected by the matrix
corrected by the matrix 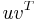 (depending on the point of view, the correction may be seen as a perturbation or as a rank-1 update). The computation is relatively cheap because the inverse of
(depending on the point of view, the correction may be seen as a perturbation or as a rank-1 update). The computation is relatively cheap because the inverse of 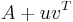 does not have to be computed from scratch (which in general is expensive), but can be computed by correcting (or perturbing)
does not have to be computed from scratch (which in general is expensive), but can be computed by correcting (or perturbing) 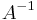 .
.
Using unit columns (columns from the identity matrix) for  or
or  , individual columns or rows of
, individual columns or rows of  may be manipulated and a correspondingly updated inverse computed relatively cheaply in this way.[6] In the general case, where
may be manipulated and a correspondingly updated inverse computed relatively cheaply in this way.[6] In the general case, where 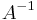 is a
is a  times
times  matrix and
matrix and  and
and  are arbitrary vectors of dimension
are arbitrary vectors of dimension  , the whole matrix is updated[5] and the computation takes
, the whole matrix is updated[5] and the computation takes 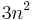 scalar multiplications.[7] If
scalar multiplications.[7] If  is a unit column, the computation takes only
is a unit column, the computation takes only 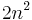 scalar multiplications. The same goes if
scalar multiplications. The same goes if  is a unit column. If both
is a unit column. If both  and
and  are both unit columns, the computation takes only
are both unit columns, the computation takes only 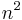 scalar multiplications.
scalar multiplications.
Verification
We verify the properties of the inverse. A matrix  (in this case the right-hand side of the Sherman–Morrison formula) is the inverse of a matrix
(in this case the right-hand side of the Sherman–Morrison formula) is the inverse of a matrix  (in this case
(in this case 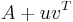 ) if and only if
) if and only if 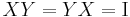 .
.
We first verify that the right hand side ( ) satisfies
) satisfies 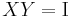 .
.
Note that 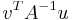 is a scalar, so
is a scalar, so 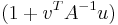 can be factored out, leading to:
can be factored out, leading to:
In the same way, it is verified that
Following is an alternate verification of the Sherman–Morrison formula using the easily verifiable identity
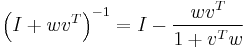
Let 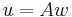 and
and 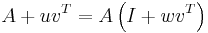 , then
, then
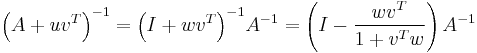
Substituting 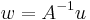 gives
gives
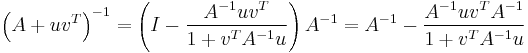
See also
- The matrix determinant lemma performs a rank-1 update to a determinant.
- Sherman–Morrison–Woodbury formula
- Quasi-Newton method
- Binomial inverse theorem
References
- ^ Sherman, Jack; Morrison, Winifred J. (1949). "Adjustment of an Inverse Matrix Corresponding to Changes in the Elements of a Given Column or a Given Row of the Original Matrix (abstract)". Annals of Mathematical Statistics 20: 621. doi:10.1214/aoms/1177729959.
- ^ Sherman, Jack; Morrison, Winifred J. (1950). "Adjustment of an Inverse Matrix Corresponding to a Change in One Element of a Given Matrix". Annals of Mathematical Statistics 21 (1): 124–127. doi:10.1214/aoms/1177729893. MR35118. Zbl 0037.00901.
- ^ Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 2.7.1 Sherman-Morrison Formula", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, http://apps.nrbook.com/empanel/index.html?pg=76
- ^ Hager, William W. (1989). "Updating the inverse of a matrix". SIAM Review 31 (2): 221–239. doi:10.1137/1031049. JSTOR 2030425. MR997457.
- ^ a b Bartlett, M. S. (1951). "An Inverse Matrix Adjustment Arising in Discriminant Analysis". Annals of Mathematical Statistics 22 (1): 107–111. doi:10.1214/aoms/1177729698. MR40068. Zbl 0042.38203.
- ^ Langville, Amy N. and Meyer, Carl D., "Google's PageRank and Beyond: The Science of Search Engine Rankings", Princeton University Press, 2006, p. 156
- ^ Update of the inverse matrix by the Sherman-Morrison formula